Olá a todos!
Sejam bem vindos a este projeto de aulas virtuais na disciplina de matemática para o 3º ano. Espero que todos estejam bem e ansiosos por aprender mais dessa ciência tão fascinante.
Inicialmente, gostaria de preencher algumas lacunas e relembrar conceitos importantes que iremos utilizar ao longo da etapa final do Ensino Médio. A primeira habilidade a ser trabalhada está pautada na Álgebra Linear e suas aplicações.
Abaixo, sugiro uma lista de vídeos pedagógicos da Prof. Angela e do Prof. Procópio, os quais considero bastante adequados, com excelente didática e conteúdos bem desenvolvidos. Futuramente, estarei postando meus próprios vídeos sobre o assunto das aulas e resolução dos exercícios propostos.
Bons estudos!
Dúvidas, podem entrar em contato pelos email:
ricardosalves@prof.educacao.sp.gov.br
DETERMINANTE DE MATRIZES
Notação para determinantes de matrizes
Seja a matriz M a seguir:
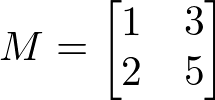
Definimos determinantes de M como det (M) ou
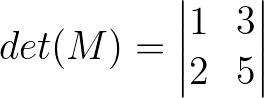
Determinante de matriz de ordem 1
O determinate de uma matriz de ordem 1×1 é o próprio elemento da matriz.
Exemplo:
- A = [1] ⇒ det A = 1
Determinante de matriz de ordem 2
O determinante das matrizes quadradas – aquelas que possuem os mesmo números de linhas e colunas – de ordem 2×2 é calculado pela multiplicação dos elementos da diagonal principal e secundária. Assim:
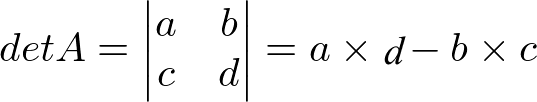
Exemplo:
Seja a matriz M:
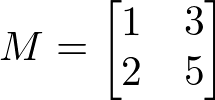
Então:
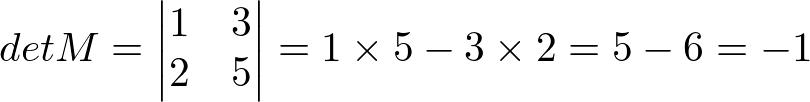
Determinantes de matriz de ordem 3
Para calcularmos o determinante de uma matriz quadrada de ordem 3×3 temos que utilizar a regra de Sarrus. Veja como:
Seja A uma matriz quadrada de ordem 3×3:
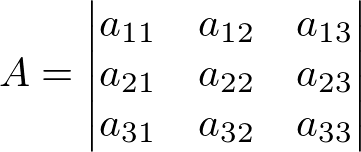
A regra de Sarrus funciona da seguinte maneira:
Copiamos a 1ª e 2ª coluna da matriz A para o lado direito da matriz, veja:
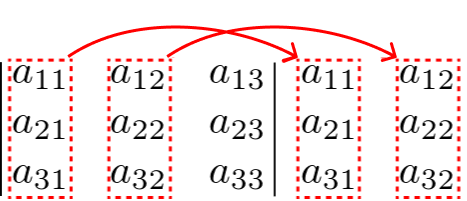
Depois fazemos o produto entre os termos da matriz com as colunas que copiamos para o lado direito, seguindo as setas abaixo: para as setas azuis, multiplicamos os 3 elementos diagonalmente e associamos os sinais de mais (+); para as setas vermelhas, multiplicamos os 3 elementos de cada seta e associamos o sinal de menos (-). Veja:

Então: det A = a11 . a22 . a33 + a12 . a23 . a31 + a13 . a21 . a32 – a13 . a22 . a31 – a11 . a23 . a32 – a12 . a21. a33
Vamos ver um exemplo prático.
Exemplo:
Considere a matriz A abaixo:

Assim, seguindo a regra de Sarrus, copiamos a 1ª e 2ª coluna de A para o lado direito:

Seguindo o sentido das setas e obedecendo os sinais, temos que:
det A = 1 . 5 . 3 + 3 . 1 . 2 + 0 . 2 . 1 – 0 . 5 . 2 – 1 . 1 . 1 – 3 . 2 . 3 = 15 + 6 + 0 – 0 – 1 – 18 = 21 – 19 = 2
Portanto, det(A) = 2
EXERCÍCIOS
1) Considere a matriz abaixo de ordem 2, calcule o seu determinante.

2) Seja a matriz A de ordem 3, calcule o seu determinante.


Respostas
1)
O determinante de uma matriz de ordem 2 é calculado multiplicando os elementos da diagonal principal com os elementos da diagonal secundária.
Portanto,
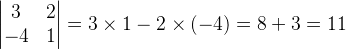
2)
Matrizes de ordem 3 podemos calcular o determinante usando a regra de Sarrus. Assim:
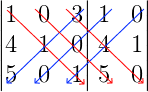
(1 x 1 x 1) + (0 x 0 x 5) + (3 x 4 x 0) – (5 x 1 x 3) – (0 x 0 x 1) – (1 x 4 x 0) = -14
Portanto, o det(A) = – 14
Bibliografia
NOVAES, Jean Carlos. Matemática Básica - Matrizes e determinantes. Disponível em <https://matematicabasica.net/exercicios-sobre-matrizes-e-determinantes/>. Acesso dia 26/04/2020.


Comentários
Postar um comentário